Sai che aspetto ha un esagono regolare?
Questa domanda non è stata posta per caso. La maggior parte degli studenti dell'undicesimo anno non conosce la risposta a questa domanda.
Un esagono regolare è quello in cui tutti i lati sono uguali e anche tutti gli angoli sono uguali..
Noce di ferro. Fiocco di neve. Cella di un favo in cui vivono le api. Molecola di benzene. Cosa hanno in comune questi oggetti? - Il fatto che abbiano tutti una forma esagonale regolare.
Molti scolari si confondono quando vedono problemi che coinvolgono un esagono regolare e credono che siano necessarie alcune formule speciali per risolverli. È così?
Disegniamo le diagonali di un esagono regolare. Abbiamo sei triangoli equilateri.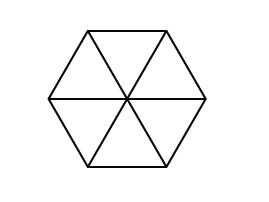 
Sappiamo che l'area di un triangolo regolare è: .
Quindi l'area di un esagono regolare è sei volte maggiore.
Dov'è il lato di un esagono regolare.
Tieni presente che in un esagono regolare, la distanza dal suo centro a uno qualsiasi dei vertici è la stessa ed è uguale al lato dell'esagono regolare.
Ciò significa che il raggio di un cerchio circoscritto ad un esagono regolare è uguale al suo lato.
Il raggio di un cerchio inscritto in un esagono regolare non è difficile da trovare.
È uguale.
Ora puoi risolverne facilmente qualsiasi Compiti dell'Esame di Stato Unificato, in cui appare un esagono regolare.
Trovare il raggio di un cerchio inscritto in un esagono regolare di lato .
Il raggio di tale cerchio è uguale a .
Risposta: .
Qual è il lato di un esagono regolare inscritto in una circonferenza di raggio 6?
Sappiamo che il lato di un esagono regolare è uguale al raggio del cerchio ad esso circoscritto.
Costruzione di un esagono regolare inscritto in una circonferenza. La costruzione di un esagono si basa sul fatto che il suo lato è uguale al raggio del cerchio circoscritto. Pertanto, per costruirlo, è sufficiente dividere il cerchio in sei parti uguali e collegare tra loro i punti trovati (Fig. 60, a).
È possibile costruire un esagono regolare utilizzando un bordo dritto e un quadrato 30X60°. Per eseguire questa costruzione, prendiamo il diametro orizzontale del cerchio come bisettrice degli angoli 1 e 4 (Fig. 60, b), costruiamo i lati 1 -6, 4-3, 4-5 e 7-2, dopo di che disegniamo i lati 5-6 e 3-2.
Costruzione di un triangolo equilatero inscritto in una circonferenza. I vertici di un tale triangolo possono essere costruiti utilizzando un compasso e una squadra con angoli di 30 e 60° oppure utilizzando un solo compasso.
Consideriamo due modi per costruire un triangolo equilatero inscritto in una circonferenza.
Primo modo(Fig. 61,a) si basa sul fatto che tutti e tre gli angoli del triangolo 7, 2, 3 contengono 60°, e la linea verticale tracciata attraverso il punto 7 è sia l'altezza che la bisettrice dell'angolo 1. Poiché l'angolo è 0-1- 2 è uguale a 30°, quindi trovare il lato
1-2, è sufficiente costruire un angolo di 30° dal punto 1 e dal lato 0-1. Per fare ciò, installa la traversa e il quadrato come mostrato nella figura, traccia la linea 1-2, che sarà uno dei lati del triangolo desiderato. Per costruire i lati 2-3, posiziona la traversa nella posizione mostrata dalle linee tratteggiate e traccia una linea retta attraverso il punto 2, che determinerà il terzo vertice del triangolo.
Secondo modo si basa sul fatto che se costruisci un esagono regolare inscritto in una circonferenza e poi unisci i suoi vertici attraverso uno di essi, otterrai un triangolo equilatero.
Per costruire un triangolo (Fig. 61, b), segnare il vertice 1 sul diametro e tracciare una linea diametrale 1-4. Successivamente, dal punto 4 con raggio pari a D/2, descriviamo un arco fino ad intersecare il cerchio nei punti 3 e 2. I punti risultanti saranno gli altri due vertici del triangolo desiderato.
Costruzione di un quadrato inscritto in una circonferenza. Questa costruzione può essere eseguita utilizzando una squadra e un compasso.
Il primo metodo si basa sul fatto che le diagonali del quadrato si intersecano al centro del cerchio circoscritto e sono inclinate rispetto al suo asse di un angolo di 45°. Su questa base installiamo la traversa e la squadra con angoli di 45° come mostrato in Fig. 62, a, e segniamo i punti 1 e 3. Successivamente, attraverso questi punti disegniamo i lati orizzontali del quadrato 4-1 e 3-2 usando una traversa. Quindi, utilizzando un righello, disegniamo i lati verticali del quadrato 1-2 e 4-3 lungo la gamba del quadrato.
Il secondo metodo si basa sul fatto che i vertici del quadrato dividono in due gli archi di cerchio racchiusi tra le estremità del diametro (Fig. 62, b). Segniamo i punti A, B e C alle estremità di due diametri reciprocamente perpendicolari e da essi con raggio y descriviamo archi finché non si intersecano tra loro.
Successivamente, attraverso i punti di intersezione degli archi tracciamo linee rette ausiliarie, contrassegnate nella figura con linee continue. I punti della loro intersezione con il cerchio determineranno i vertici 1 e 3; 4 e 2. Colleghiamo in serie tra loro i vertici del quadrato desiderato così ottenuto.
Costruzione di un pentagono regolare inscritto in una circonferenza.
Per inserire un pentagono regolare in un cerchio (Fig. 63), realizziamo le seguenti costruzioni.
Segniamo il punto 1 sul cerchio e prendiamolo come uno dei vertici del pentagono. Dividiamo il segmento AO a metà. Per fare ciò descriviamo un arco dal punto A di raggio AO fino a quando non interseca il cerchio nei punti M e B. Collegando questi punti con una linea retta otteniamo il punto K, che colleghiamo poi al punto 1. Con un raggio pari al segmento A7, descriviamo un arco dal punto K fino ad intersecare la linea diametrale AO nel punto H. Collegando il punto 1 con il punto H, otteniamo il lato del pentagono. Quindi, utilizzando una soluzione compasso pari al segmento 1H, descrivendo un arco dal vertice 1 all'intersezione con il cerchio, troviamo i vertici 2 e 5. Avendo fatto degli intagli dai vertici 2 e 5 con la stessa soluzione compasso, otteniamo il restante vertici 3 e 4. Colleghiamo i punti trovati in sequenza tra loro.
Costruire un pentagono regolare lungo un dato lato.
Per costruire un pentagono regolare lungo un dato lato (Fig. 64), dividiamo il segmento AB in sei parti uguali. Dai punti A e B con raggio AB descriviamo archi, la cui intersezione darà il punto K. Attraverso questo punto e la divisione 3 sulla linea AB tracciamo una linea verticale.
Otteniamo il punto 1-vertice del pentagono. Quindi, con raggio pari ad AB, dal punto 1 descriviamo un arco fino ad intersecare gli archi precedentemente disegnati dai punti A e B. I punti di intersezione degli archi determinano i vertici 2 e 5 del pentagono. Colleghiamo i vertici trovati in serie tra loro.
Costruzione di un ettagono regolare inscritto in una circonferenza.
Sia dato un cerchio di diametro D; è necessario inserire un ettagono regolare al suo interno (Fig. 65). Dividi il diametro verticale del cerchio in sette parti uguali. Dal punto 7 di raggio pari al diametro del cerchio D, descriviamo un arco finché non si interseca con la continuazione del diametro orizzontale nel punto F. Chiameremo il punto F polo del poligono. Prendendo il punto VII come uno dei vertici dell'ettagono, tracciamo i raggi dal polo F attraverso divisioni pari del diametro verticale, la cui intersezione con il cerchio determinerà i vertici VI, V e IV dell'ettagono. Per ottenere i vertici / - // - /// dai punti IV, V e VI, tracciare linee orizzontali finché non si intersecano con il cerchio. Colleghiamo i vertici trovati in sequenza tra loro. Un ettagono può essere costruito traendo raggi dal polo F e attraverso divisioni dispari del diametro verticale.
Il metodo sopra è adatto per costruire poligoni regolari con qualsiasi numero di lati.
La divisione di un cerchio in un numero qualsiasi di parti uguali può essere eseguita anche utilizzando i dati nella tabella. 2, che fornisce coefficienti che permettono di determinare le dimensioni dei lati dei poligoni regolari inscritti.
Proprietà matematiche
La particolarità di un esagono regolare è l'uguaglianza del suo lato e del raggio del cerchio circoscritto, poiché
Tutti gli angoli sono uguali a 120°.
Il raggio del cerchio inscritto è uguale a:
Il perimetro di un esagono regolare è:
L'area di un esagono regolare viene calcolata utilizzando le formule:
Gli esagoni affiancano un piano, cioè possono riempire un piano senza vuoti o sovrapposizioni, formando il cosiddetto parquet.
Parquet esagonale (parquet esagonale)- piastrellatura di un piano con esagoni regolari uguali disposti affiancati.
Il parquet esagonale è duale rispetto al parquet triangolare: se colleghi i centri di esagoni adiacenti, i segmenti disegnati daranno un parquet triangolare. Il simbolo Schläfli per un parquet esagonale è (6,3), il che significa che su ciascun vertice del parquet si incontrano tre esagoni.
Il parquet esagonale è l'imballaggio più denso di cerchi su un piano. Nello spazio euclideo bidimensionale, il riempimento migliore consiste nel posizionare i centri dei cerchi ai vertici di un parquet formato da esagoni regolari, in cui ogni cerchio è circondato da altri sei. La densità di questo pacchetto è . Nel 1940 fu dimostrato che questo imballaggio è il più denso.
Un esagono regolare con un lato è una copertura universale, cioè qualsiasi insieme di diametri può essere coperto da un esagono regolare con un lato (lemma di Pala).
Un esagono regolare può essere costruito utilizzando compasso e righello. Di seguito è riportato il metodo di costruzione proposto da Euclide negli Elementi, Libro IV, Teorema 15.
Esagono regolare nella natura, nella tecnologia e nella cultura
mostrano la divisione del piano in esagoni regolari. La forma esagonale consente di risparmiare sui muri più di altri, ovvero sui favi con tali celle verrà spesa meno cera.
Alcuni cristalli e molecole complessi, come la grafite, hanno un reticolo cristallino esagonale.
Si forma quando microscopiche goccioline d'acqua nelle nuvole vengono attratte dalle particelle di polvere e si congelano. I cristalli di ghiaccio che compaiono, inizialmente non superiori a 0,1 mm di diametro, cadono e crescono a causa della condensazione dell'umidità dell'aria su di essi. Questo produce forme cristalline a sei punte. A causa della struttura delle molecole d'acqua, tra i raggi del cristallo sono possibili angoli di soli 60° e 120°. Il cristallo d'acqua principale ha la forma di un esagono regolare nel piano. Nuovi cristalli vengono quindi depositati sui vertici di tale esagono e su di essi ne vengono depositati di nuovi, ed è così che si ottengono varie forme di stelle fiocco di neve.
Gli scienziati dell'Università di Oxford sono stati in grado di simulare l'aspetto di un simile esagono in condizioni di laboratorio. Per scoprire come avviene questa formazione, i ricercatori hanno posizionato una bottiglia d'acqua da 30 litri su un tavolo rotante. Simulava l'atmosfera di Saturno e la sua normale rotazione. All'interno, gli scienziati hanno posizionato piccoli anelli che ruotano più velocemente del contenitore. Ciò ha generato vortici e getti in miniatura, che gli sperimentatori hanno visualizzato utilizzando vernice verde. Quanto più velocemente l'anello ruotava, tanto più grandi diventavano i vortici, facendo deviare il flusso vicino dalla sua forma circolare. In questo modo, gli autori dell'esperimento sono riusciti a ottenere varie forme: ovali, triangoli, quadrati e, ovviamente, l'esagono desiderato.
Un monumento naturale di circa 40.000 colonne di basalto (meno spesso andesite) interconnesse formatesi a seguito di un'antica eruzione vulcanica. Situato nel nord-est dell'Irlanda del Nord, 3 km a nord della città di Bushmills.
Le sommità delle colonne formano una sorta di trampolino di lancio, che inizia ai piedi della scogliera e scompare sotto la superficie del mare. La maggior parte delle colonne sono esagonali, anche se alcune hanno quattro, cinque, sette e otto angoli. La colonna più alta è alta circa 12 m.
Circa 50-60 milioni di anni fa, durante il periodo Paleogene, il sito di Antrim fu soggetto ad un'intensa attività vulcanica poiché il basalto fuso penetrò nei sedimenti per formare estesi altipiani lavici. Man mano che la sostanza si raffreddava rapidamente, il volume della sostanza diminuiva (una cosa simile si osserva quando il fango si asciuga). La compressione orizzontale ha prodotto una caratteristica struttura a pilastri esagonali.
La sezione trasversale del dado ha la forma di un esagono regolare.
Sai che aspetto ha un esagono regolare?
Questa domanda non è stata posta per caso. La maggior parte degli studenti dell'undicesimo anno non conosce la risposta a questa domanda.
Un esagono regolare è quello in cui tutti i lati sono uguali e anche tutti gli angoli sono uguali..
Noce di ferro. Fiocco di neve. Cella di un favo in cui vivono le api. Molecola di benzene. Cosa hanno in comune questi oggetti? - Il fatto che abbiano tutti una forma esagonale regolare.
Molti scolari si confondono quando vedono problemi che coinvolgono un esagono regolare e credono che siano necessarie alcune formule speciali per risolverli. È così?
Disegniamo le diagonali di un esagono regolare. Abbiamo sei triangoli equilateri.
Sappiamo che l'area di un triangolo regolare è: .
Quindi l'area di un esagono regolare è sei volte maggiore.
Dov'è il lato di un esagono regolare.
Tieni presente che in un esagono regolare, la distanza dal suo centro a uno qualsiasi dei vertici è la stessa ed è uguale al lato dell'esagono regolare.
Ciò significa che il raggio di un cerchio circoscritto ad un esagono regolare è uguale al suo lato.
Il raggio di un cerchio inscritto in un esagono regolare non è difficile da trovare.
È uguale.
Ora puoi risolvere facilmente qualsiasi problema USE che coinvolga un esagono regolare.
Trovare il raggio di un cerchio inscritto in un esagono regolare di lato .
Il raggio di tale cerchio è uguale a .
Risposta: .
Qual è il lato di un esagono regolare inscritto in una circonferenza di raggio 6?
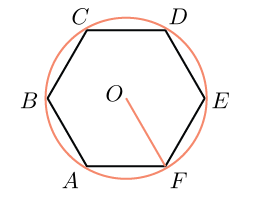
Sappiamo che il lato di un esagono regolare è uguale al raggio del cerchio ad esso circoscritto.
La figura più famosa con più di quattro angoli è un esagono regolare. In geometria è spesso usato nei problemi. E nella vita, questo è esattamente l'aspetto dei favi quando vengono tagliati.
In cosa è diverso da quello sbagliato?
Innanzitutto, un esagono è una figura con 6 vertici. In secondo luogo, può essere convesso o concavo. Il primo è diverso in quanto quattro vertici giacciono su un lato di una linea retta passante per gli altri due.
In terzo luogo, un esagono regolare è caratterizzato dal fatto che tutti i suoi lati sono uguali. Inoltre, anche ogni angolo della figura ha lo stesso significato. Per determinare la somma di tutti i suoi angoli, dovrai utilizzare la formula: 180º * (n - 2). Qui n è il numero di vertici della figura, cioè 6. Un semplice calcolo dà un valore di 720º. Cioè, ogni angolo è uguale a 120 gradi.
Nelle attività quotidiane, l'esagono regolare si trova nel fiocco di neve e nella noce. I chimici lo vedono anche nella molecola del benzene.
Quali proprietà devi conoscere quando risolvi i problemi?
A quanto sopra esposto vanno aggiunti:
- le diagonali della figura tracciata per il centro la dividono in sei triangoli equilateri;
- il lato di un esagono regolare ha un valore che coincide con il raggio del cerchio ad esso circoscritto;
- Usando una figura del genere, è possibile riempire l'aereo e non ci saranno spazi tra loro né sovrapposizioni.
Designazioni introdotte
Tradizionalmente, il lato di una figura geometrica regolare è indicato con la lettera latina “a”. Per risolvere i problemi sono necessari anche l'area e il perimetro, rispettivamente S e P. Un cerchio può essere inscritto in un esagono regolare oppure descritto attorno ad esso. Quindi vengono inseriti i valori per i loro raggi. Sono designati rispettivamente dalle lettere r e R.
Alcune formule includono un angolo interno, un semiperimetro e un apotema (che è perpendicolare al centro di qualsiasi lato dal centro del poligono). Le lettere utilizzate per loro sono: α, р, m.
Formule che descrivono una figura
Per calcolare il raggio di una circonferenza inscritta avrai bisogno di: r = (a*√3)/2, con r = m. Cioè, la stessa formula sarà per l'apotema.
Poiché il perimetro di un esagono è la somma di tutti i lati, verrà determinato come segue: P = 6 * a. Tenendo conto del fatto che il lato è uguale al raggio del cerchio inscritto, per il perimetro vale la seguente formula per un esagono regolare: P = 6 * R. Da quella data per il raggio del cerchio inscritto, la viene derivata la relazione tra a e r. Allora la formula assume la seguente forma: P = 4 r * √3.
Per l'area di un esagono regolare può essere utile: S = p * r = (a 2 * 3 √3) / 2.
Compiti
N. 1. Condizione. C'è un prisma esagonale regolare, i cui spigoli misurano rispettivamente 4 cm e in esso è inscritto un cilindro, il cui volume deve essere trovato.
Soluzione. Il volume di un cilindro è definito come il prodotto dell'area della base e dell'altezza. Quest'ultimo coincide con il bordo del prisma. Ed è uguale al lato di un esagono regolare. Cioè, anche l'altezza del cilindro è di 4 cm.
Per scoprire l'area della sua base, dovrai calcolare il raggio del cerchio inscritto nell'esagono. La formula per questo è data sopra. Ciò significa r = 2√3 (cm). Quindi l'area del cerchio: S = π * r 2 = 3,14 * (2√3) 2 = 37,68 (cm 2).
Risposta. V = 150,72 cm3.
N. 2. Condizione. Calcola il raggio di una circonferenza inscritta in un esagono regolare. Sappiamo che il suo lato è √3 cm, a quanto sarà uguale il suo perimetro?
Soluzione. Questo problema richiede l'uso di due delle seguenti formule. Inoltre vanno applicati senza nemmeno modificarli, basta sostituire il valore del lato e calcolare.
Pertanto il raggio del cerchio inscritto è pari a 1,5 cm, per il perimetro risulta corretto il valore: 6√3 cm.
Risposta. r = 1,5 cm, P = 6√3 cm.
N. 3. Condizione. Il raggio del cerchio circoscritto è 6 cm. Che valore avrà il lato di un esagono regolare in questo caso?
Soluzione. Dalla formula del raggio di un cerchio inscritto in un esagono si ottiene facilmente quella con cui bisogna calcolare il lato. È chiaro che il raggio viene moltiplicato per due e diviso per la radice di tre. È necessario eliminare l'irrazionalità nel denominatore. Pertanto, il risultato delle azioni assume la seguente forma: (12 √3) / (√3 * √3), cioè 4√3.
Risposta. a = 4√3 cm.